归并排序

归并排序（英语：Merge sort，或mergesort），是创建在归并操作上的一种有效的排序算法，效率为O(NlgN)。
1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。

自顶向下的归并排序

递归实现的归并排序是算法设计中分治思想的典型应用。

/**
 *  <p>归并排序
 *
 *  <p>自顶向下
 *
 *  <p>时间复杂度: O(1/2NlgN)到O(NlgN)
 *  <p>空间复杂度: O(N)
 *
 * @author teaho2015@gmail.com
 */
public class MergeSort1 {

    public void sort(Comparable[] arr) {
        Comparable[] temp = new Comparable[arr.length];

        sort(arr, 0, arr.length - 1, temp);
    }

    public void sort(Comparable[] arr, int lf, int rt, Comparable[] temp) {

        if (lf >= rt) {
            return;
        }
        int mid = (lf + rt) / 2;
        //左边
        sort(arr, lf, mid, temp);
        //右边
        sort(arr, mid + 1, rt, temp);
        merge(arr, lf, mid, rt, temp);
    }


    public void merge(Comparable[] arr, int lf, int mid, int rt, Comparable[] temp) {

        int i = lf, j = mid + 1;
        for (int k = lf; k <= rt; k++) {
            temp[k] = arr[k];
        }

        for (int k = lf; k <= rt; k++) {
            if (i > mid) {
                arr[k] = temp[j++];
            } else if(j > rt) {
                arr[k] = temp[i++];
            } else if (temp[i].compareTo(temp[j]) < 0) {
                arr[k] = temp[i++];
            } else {
                arr[k] = temp[j++];
            }
        }

    }
}

自底向上的归并排序

自底向上的实现是通过迭代实现。

/**
 * <p>归并排序
 *
 * <p>自底向上的方式
 *
 *  <p>时间复杂度: O(1/2NlgN)到O(NlgN)
 *  <p>空间复杂度: O(N)
 *
 * @author teaho2015@gmail.com
 */
public class MergeSort2 {


    public void sort(Comparable[] arr) {

        //进行lgN此两两归并
        int len = arr.length;
        Comparable[] temp = new Comparable[arr.length];
        //sz为划分子数组的长度
        for (int sz = 1; sz < len; sz += sz) {
            for (int i = 0; i < len - sz; i += (sz + sz)) {
                merge(arr, i, i + sz - 1, Math.min(i + sz + sz - 1, len - 1), temp);
            }
        }


    }

    public void merge(Comparable[] arr, int lf, int mid, int rt, Comparable[] temp) {

        int i = lf, j = mid + 1;
        for (int k = lf; k <= rt; k++) {
            temp[k] = arr[k];
        }

        for (int k = lf; k <= rt; k++) {
            if (i > mid) {
                arr[k] = temp[j++];
            } else if(j > rt) {
                arr[k] = temp[i++];
            } else if (temp[i].compareTo(temp[j]) < 0) {
                arr[k] = temp[i++];
            } else {
                arr[k] = temp[j++];
            }
        }

    }
}

排序算法的复杂度

在《算法》[1]一书中在归并排序一节谈到一个研究排序算法复杂度的案例。挺值得一说。

命题：没有任何基于比较的算法能够保证使用少于lg(N!)~NlgN次比较将长度为N的数组排序。

证明： 首先，假设没有重复的主键，因为任何排序算法在该情况下讨论才有意义。 我们使用如下二叉树来表示所有比较，假设元素个数为N=3：

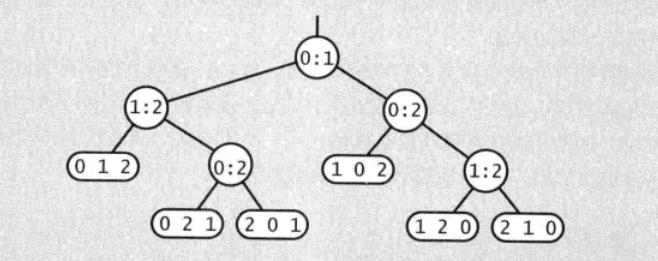
树中的节点：

• 一般节点：i:j，表示a[i]和a[j]之间的比较操作。
• 叶子节点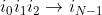：表示元素原顺序的最终排序结果。

我们从来没明确构造这棵树，它只是用来描述算法中比较的一个数学工具。 从这棵比较树我们可以得出结论，

• 这棵树至少有N!个树叶节点。因为N个主键会有N！种排列方式。
• 而从二叉树的性质出发来看，一个高h的二叉树最多可能有2^h个叶子结点。（即完全树的情况）

所以得出结论： N! <= 叶子结点数量 <= 2^h

h的值就是最坏情况下的比较次数，因此对不等式的两边取对数即可得到任意算法的比较次数至少是lgN!。 根据斯特宁公式对阶乘函数的近似可得路径（即排序比较次数）为： lgN!~NlgN

References

[1]Robert Sedgewick,Kevin Wayne.算法（第4版）.中国：人民邮电出版社,2012 [2]归并排序|维基百科